Research
Our research focuses on data-driven engineering and uncertainty quantification (UQ). Data-driven engineering is the incorporation of advanced data analytic techniques into the traditional, physics-based analysis of engineering systems. Uncertainty quantification is the assessment of various types of errors and uncertainties in such computational analyses. There has been a surge of interest in connecting physics and data for engineering problems, and what makes our work unique is the pursuit of fast, reliable, and interpretable methods.
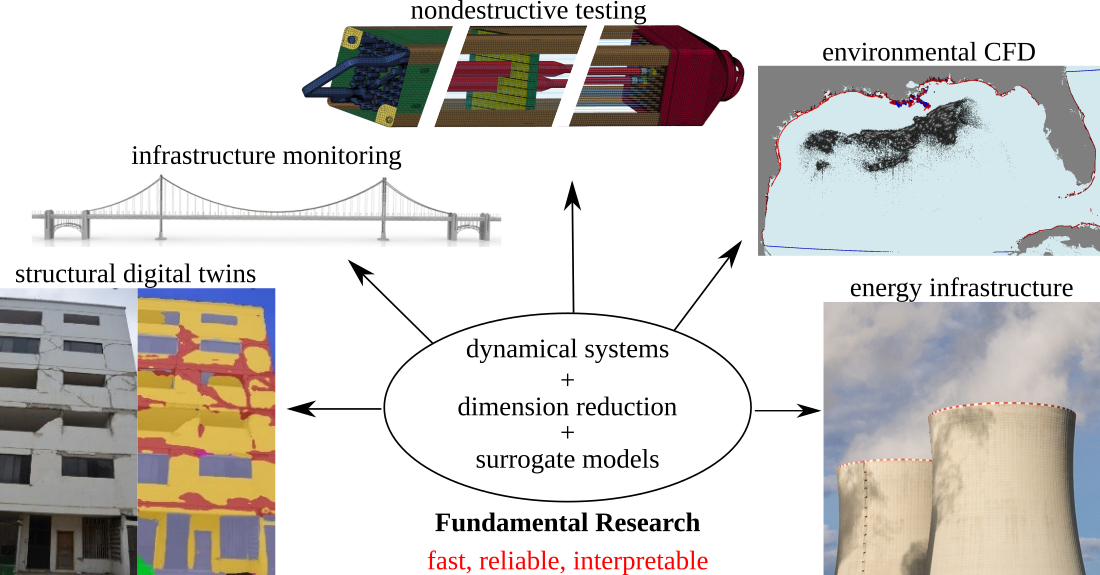
(Image credits: Johann Guilleminot, Vedhus Hoskere.)
The research framework (see Figure) involves fundamental methodology and engineering applications. The fundamentals combine dynamical systems with techniques for dimension reduction and surrogate modeling. This combination makes it possible to design methods that are: (1) fast, i.e. can complete a task in a desirable time range, either for real-time operation and control or for off-line design and analysis; (2) reliable, i.e. have theoretical guarantees about model accuracy; and (3) interpretable, i.e. be transparent enough so that people know how the model works. Applications of interest include: (1) structural digital twins such as for buildings and bridges; (2) health monitoring of civil infrastructure, e.g. via remote sensing technologies; (3) computation-assisted analysis of structural systems, e.g. non-destructive testing of waste nuclear fuel containers; (4) quantitative sustainability and resilience against hazards and climate change, based on computational fluid dynamics of the environment; (5) reliability analysis of infrastructure systems for sustainable energy, e.g. to improve the safety and economic efficiency of power plants.
UQ for ROM-based Digital Twins
To enable real-time prediction, digital twins often use reduced order models (ROMs) derived from large-scale computational models of the corresponding physical asset. Such models trade accuracy for prediction speed, while the error introduced is often hard to estimate. This is particularly unsatisfactory when we need to make reliable decisions for critical tasks. For online prediction with truthful fidelity, one approach is to use a stochastic ROM that accounts for model uncertainty. We are interested in deriving stochastic versions of commonly used ROM methods. When the model varies with some parameters, more uncertainty can be introduced when predicting at new parameter values. Combining model and prediction uncertainties is necessary to give the right uncertainty guarantee. The overall method will be useful for updating structural digital twins.
Surrogate for Structured Responses
An important part of UQ is emulation, or surrogate modeling. Traditionally, the focus is on approximating functions whose responses are real numbers or vectors. But many objects in analysis have structures, such as subspaces, positive (semi-)definite and low-rank matrices, and probability distributions. Such objects come up in model reduction, data compression, and stochastic simulation. We have introduced a fast and accurate method for approximating subspace-valued functions, based on a novel use of Gaussian process (GP). Currently we are expanding this into a framework of GPs for emulating other types of structured responses, which has applications to heavy-ion collision and swirl injection.
UQ in Data-driven Engineering
Data-driven engineering typically uses machine learning and deep learning techniques to approximate the dynamical system and its solutions underlying an engineering problem, covering topics from data-driven dynamics to operator learning. Some prominent examples include dynamic mode decomposition (DMD), physics-informed neural networks (PINNs), and deep operator networks (FNOs, DeepONets). Instead of straightforward applications of machine learning techniques, ongoing interests are more focused on field-specific method development, an area also known as scientific machine learning (sciML). We are interested in analyzing the uncertainties associated with such methods and providing accuracy guarantees for the resulting models, for example, by introducing a Bayesian framework and deriving stochastic versions of these methods. This will be especially useful for real-time control of complex dynamics.